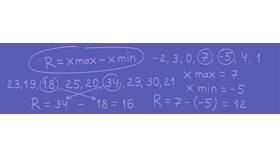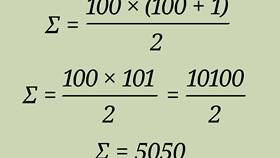Нахождение наименьшей суммы чисел - распространенная задача в математике и программировании. Рассмотрим основные подходы к ее решению:
Содержание
Основные методы поиска минимальной суммы
Полный перебор комбинаций
- Составьте список всех возможных комбинаций чисел
- Вычислите сумму для каждой комбинации
- Выберите комбинацию с минимальной суммой
Оптимизированные алгоритмы
| Алгоритм | Применение |
| Жадный алгоритм | Для последовательного выбора минимальных элементов |
| Динамическое программирование | Для сложных задач с ограничениями |
Практические примеры поиска минимальной суммы
Наименьшая сумма двух чисел
- Отсортируйте массив по возрастанию
- Сложите два первых элемента
- Альтернативно: найдите два минимальных числа без сортировки
Минимальная сумма подмассива
| Метод | Сложность |
| Полный перебор | O(n²) |
| Алгоритм Кадане | O(n) |
Математические подходы к минимизации суммы
Использование производных
Для функций: найти минимум суммы f(x) + g(x)
- Вычислите производную суммы функций
- Найдите критические точки
- Определите минимальное значение
Линейное программирование
- Сформулируйте целевую функцию минимизации
- Задайте ограничения
- Примените симплекс-метод
Программная реализация поиска
Пример на Python
| Задача | Код |
| Минимальная сумма двух чисел | min_sum = sorted(numbers)[0] + sorted(numbers)[1] |
| Наименьшая сумма подмассива | min(current_sum, min_sum = min(min_sum, current_sum)) |
Оптимизация вычислений
- Предварительная сортировка данных
- Использование хеш-таблиц для ускорения поиска
- Мемоизация промежуточных результатов
- Параллельные вычисления для больших массивов
Заключение
Поиск наименьшей суммы чисел требует понимания природы данных и выбора оптимального алгоритма. Для небольших наборов данных подходит простой перебор, тогда как для сложных задач необходимы специализированные алгоритмы. Правильный подход к решению позволяет значительно сократить вычислительные ресурсы и время обработки.